Metamaterial ideas for antennas

When using single subwavelength structures to control the scattering and emission of light, a very important consideration is what electric and magnetic multipole resonances a designed nano-object supports, and how these properties affect the scattering and emission of light. Once subwavelength objects are placed into arrays, the question is how these resonances conspire to collectively ensure a functional nano-antenna for emission, or a metasurface that shapes the wavefront or the polarization of impinging light. This knowledge can be used to realize a functional metamaterial with desired effective electric and magnetic material properties, or one with suitable diffraction effects.

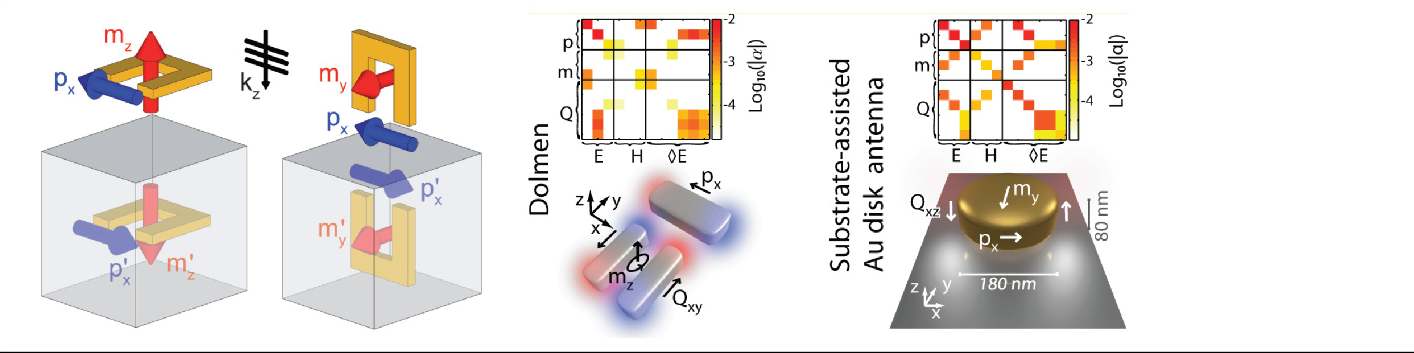
This analysis defines two essential questions in nanophotonics: how the shape and material composition of an object results in electric and magnetic multipole moments on one hand, and on the other hand how interactions between simple building blocks give interesting emergent optical properties. In our group, we perform theory and experiments in these directions. In particular, we are very interested in how shape gives rise to artificial optical magnetism, optical activity, and chiroptical effects, and how fundamental constraints such as energy conservation in scattering constrain the available degrees of freedom.

Focusing on tractable understanding with simple models for building blocks that can enter in self-consistent multiple scattering theories, we also study emergent optical scattering and emission characteristics of oligomers and lattices of building blocks. Also, we are interested in the interplay with complex surroundings, e.g. waveguides and cavities that funnel scattering, or structures that preferentially enhance magnetic or electric fields. Our theory tools include Green function methods, surface-integral equation methods, multiple scattering point dipole codes, grating and photonic crystal plane wave codes and fullwave modeling. Currently we are exploring the use of Quasi-Normal-Mode (QNM) expansion methods with the group of Lalanne.