Mathematics at the speed of light

Researchers at AMOLF, University of Pennsylvania, and City University of New York (CUNY) created a nanostructured surface capable of solving equations using light. This discovery opens exciting new opportunities in the field of analog processing based on optical metasurfaces. AMOLF PhD student Andrea Cordaro and his co-authors publish their findings in Nature Nanotechnology on January 12th 2023.
The world’s ever-growing needs for efficient computing have been driving researchers from diverse research fields to explore alternatives to the current digital computing paradigm. “The processing speed and energy efficiency of standard electronics have become limiting factors for novel disruptive applications entering our everyday life, such as artificial intelligence, machine learning, computer vision, and many more, says Andrea Cordaro. “In this context, analog computing has resurfaced and regained significant attention as a complementary route to traditional architectures.”
Computing at the speed of light
Optical analog processing refers to the use of light to perform analog computations, as opposed to traditional electronic methods which use electricity. One major benefit of using light to perform specific computing tasks is that it can operate at much higher speeds than electronic methods, as the computation is performed at the speed of light traveling through very thin nanostructured surfaces called metasurfaces. In addition, optical analog processing can be more energy efficient than electronic methods, since it does not generate heat in the same way that electronic circuits do. This makes it well-suited for use in high-performance computing applications where speed and energy efficiency are important.
“In self-driving cars, for example, image detection and processing take up a lot of computing time”, Cordaro says.
“In an earlier paper we have shown that it is possible to use an optical metasurface for very fast edge detection in an input image. Detecting the edges of objects – like cars, people etc. – is the first step in image processing in many applications. Performing this step optically can save processing time and energy.”
Matrix inversions in a jiffy
Cordaro and his colleagues realized that they could also use metasurfaces to perform other mathematical operations. “One of the most frequent class of problems popping up in many fields, including engineering, science, and economics are so-called ‘linear inverse problems’. These typically involve matrix inversions, which are rather slow mathematical operations”, he says.
The team of researchers developed a thin dielectric nanostructure, called a metagrating, and incorporated a semi-transparent mirror into the sample to continuously send back the signal to the nanostructures, each time multiplied by the metagrating scattering matrix.
“We use a special optimization technique to design the unit cell of the nanostructured array, or metagrating, that can perform the desired matrix multiplication”, says Cordaro. “Each mathematical problem requires a specific design for the metagrating, but in theory one could engineer a surface with multiple parallel gratings to solve several integral equations in parallel.”
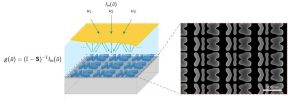
These results demonstrate the possibility of solving complex mathematical problems and a generic matrix inversion at speeds that are far beyond those of the typical digital computing methods. Indeed, the solution converges in about 349 fs (i.e., less than one thousand-millionth of a second), orders of magnitude faster than the clock speed of a conventional processor.
Cordaro: “We have shown a powerful new alliance between nanotechnology and analog computing that could pave the way for hybrid optical and electronic computing circuitry. Developing our ideas further, will result in solving problems of enhanced complexity at speed and efficiencies that were previously unthinkable.”
Reference
Andrea Cordaro, Brian Edwards, Vahid Nikkhah, Andrea Alù, Nader Engheta and Albert Polman, Solving integral equations in free space with inverse-designed ultrathin optical metagratings, Nature Nanotechnology, 12 January (2023).


